1 最小生成树
1 概念及注意
- 针对的是带权无向图
- 如果本身就是一棵树,则它的最小生成树就是本身
- 只有连通图才有生成树,非连通图只有生成森林
2 实现算法
1 Prim算法
从某一顶点开始构建生成树;每次将代价最小的新顶点纳入生成树,直到所有顶点都纳入为止
时间复杂度:O(|V|²)
适合边稠密的图
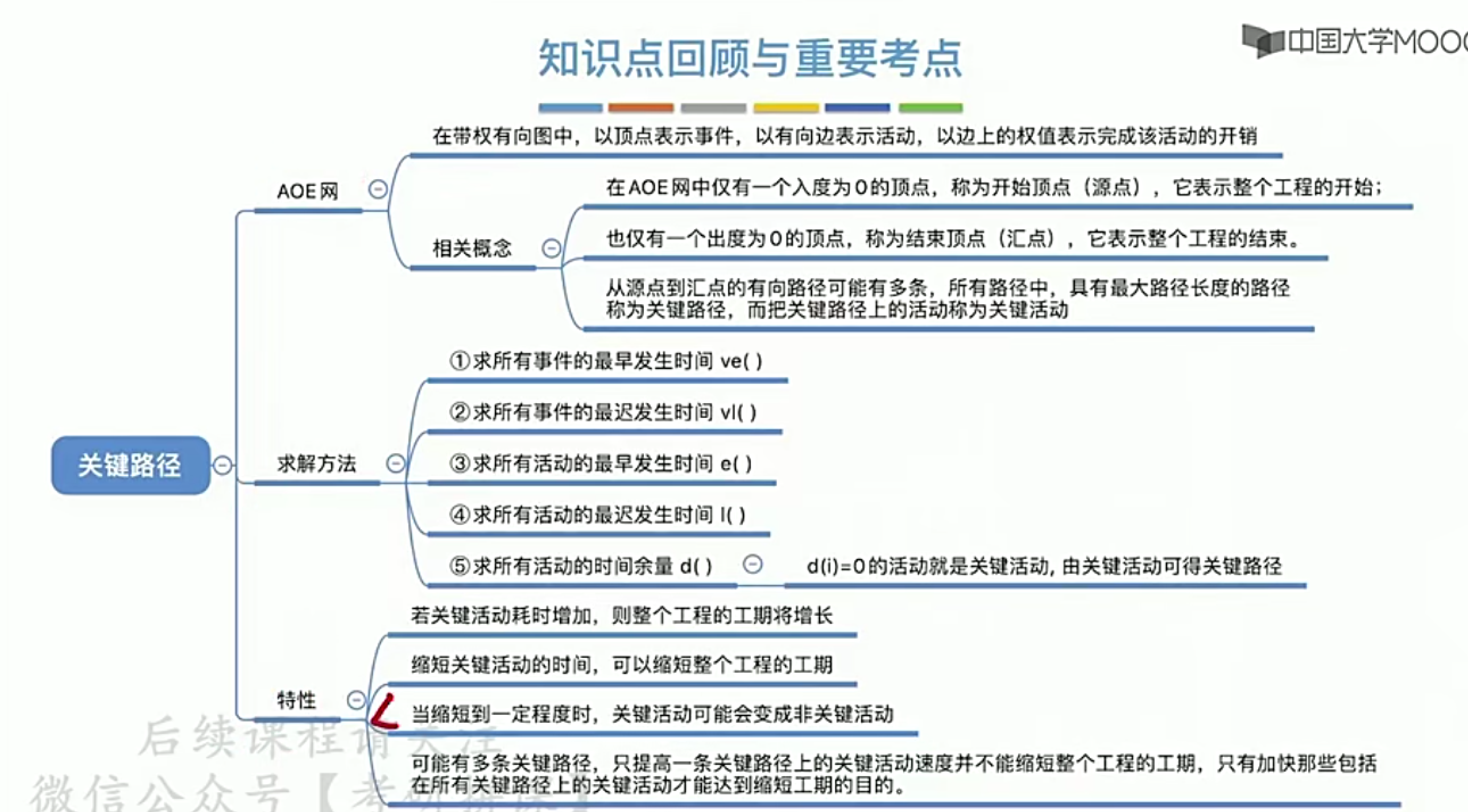
2 Kruskal算法
每次选择一条权值最小的边,使这条边的两头连通(已经连通的就不选)直到所有的结点都连通
时间复杂度:O(|E|log2|E|)
适合边稀疏而顶点较多的图

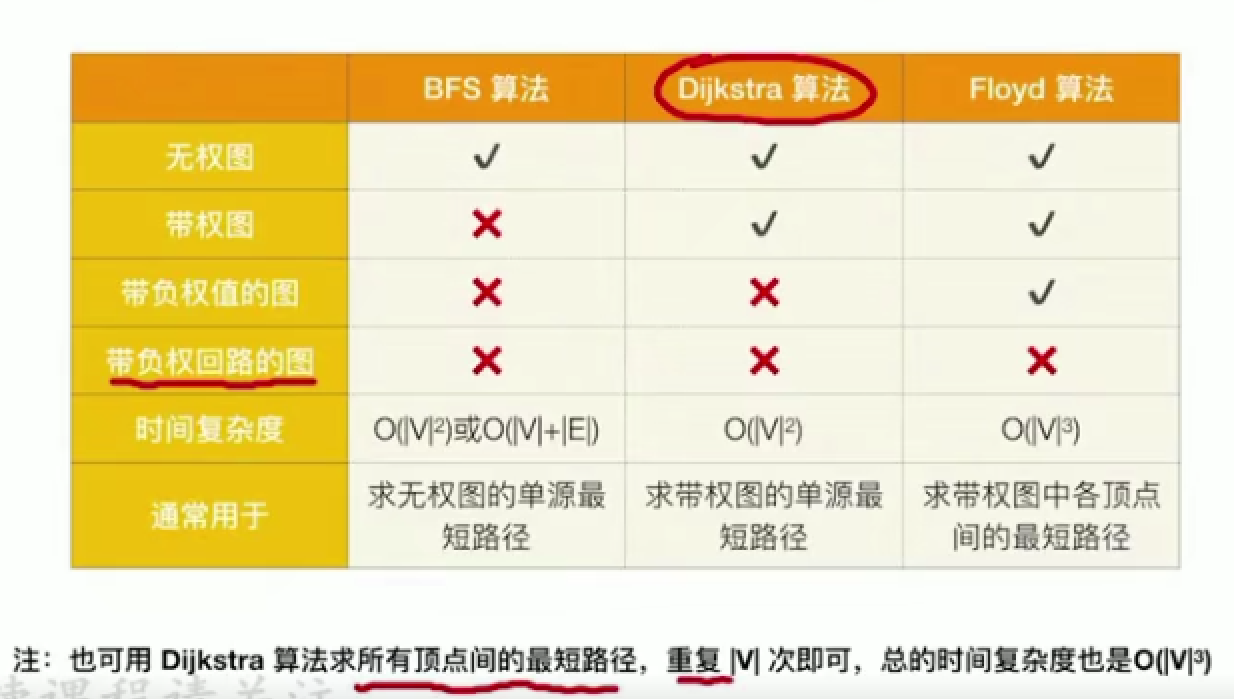
2 最短路径
分类
单源最短路径:BFS(无权图),Dijkstra算法(无权/带权)
各顶点之间的最短路径:Floyd算法(无权/带权)
当图是带权图时,一条路径上所有边的权值之和称为带权路径长度
1 BFS求最短路径
void BFS_Min_Distance(Graph G,int u)
{
for(int i=0;i<G.vexnum;i++)
{
visited[i]=false;
d[i]=∞;
p[i]=-1;
}
d[u]=0;visited[u]=true;
Queue Q;
EnQueue(Q,u);
for(w=FirstNeighbor(G,u);w>=0;w=NextNeighbor(G,u,w))
{
DeQueue(Q,u);
if(!visited[u])
{
d[w]=d[u]+1;
p[w]=u;
visited=true;
EnQueue(Q,w);
}
}
}
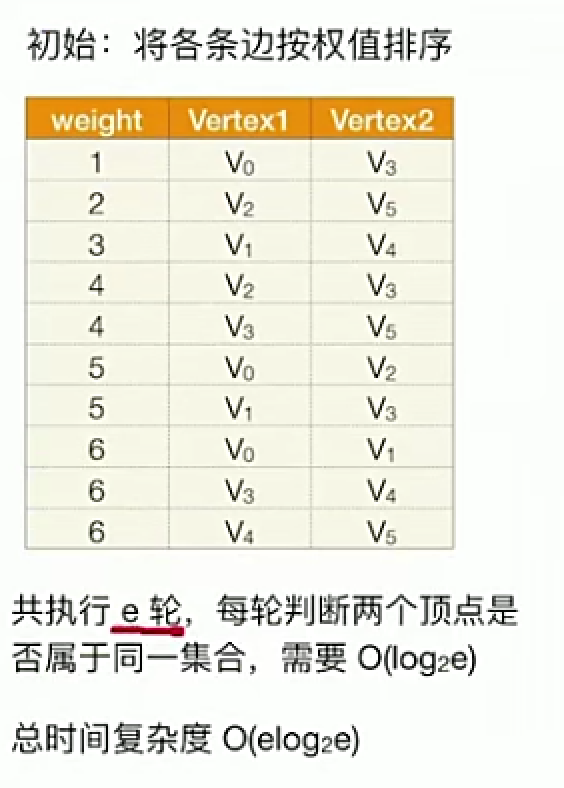
2 DijKstra算法
- 不适用于带有负权值的图
- 时间复杂度O(|V|²)
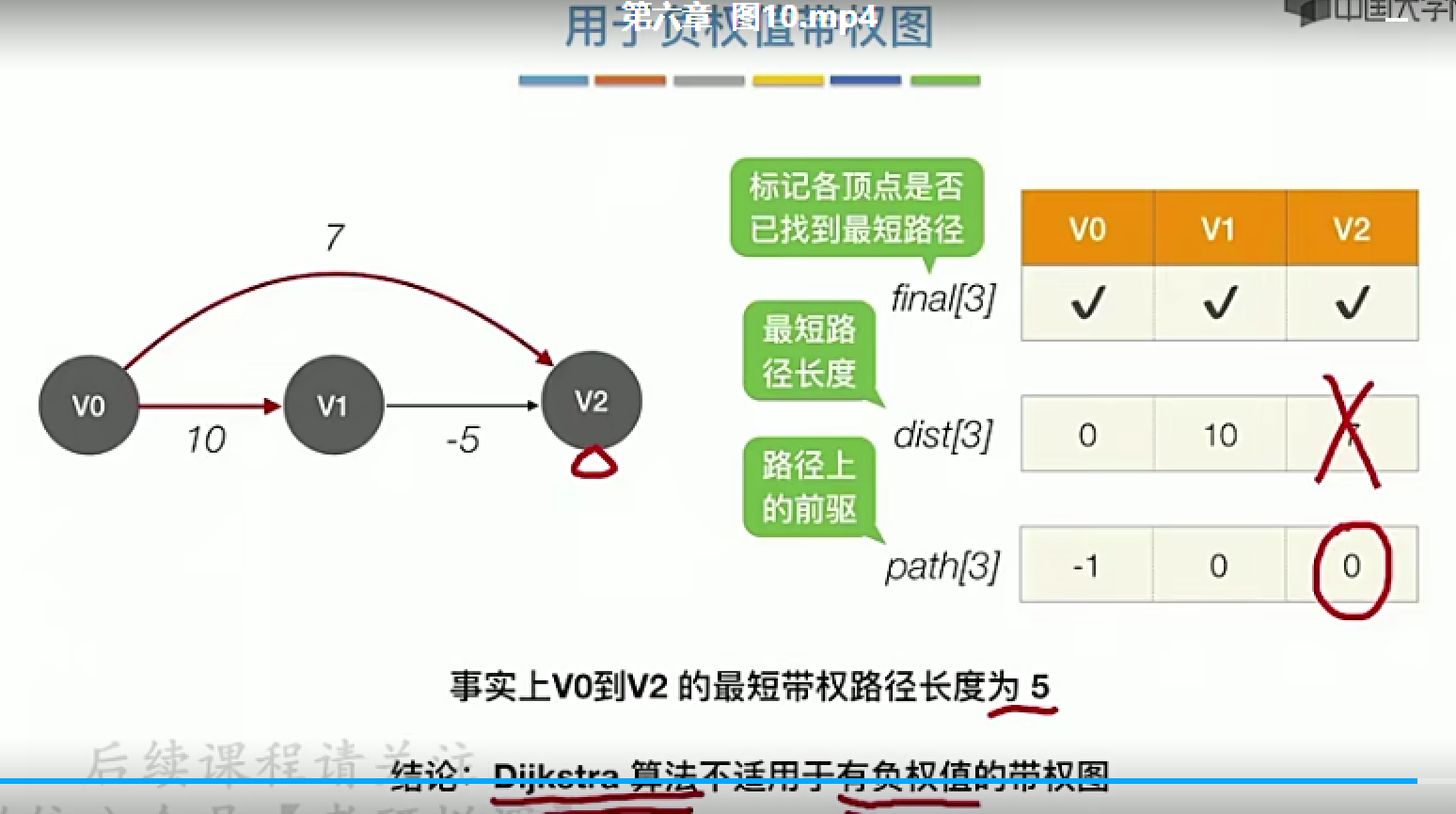
3 Floyd算法
若 A(k-1)[i] [j]> A(k-1)[i] [k]+ A(k-1)[k] [j]
则 A(k)[i] [j]=A(k-1)[i] [k]+ A(k-1)[k] [j]
Path(k)=k
否则A(k)[i] [j]和Path(k)保持原值
算法代码实现
void Floyd_Min_Distance(Graph G)
{
for(k=0;k<n;k++)
for(i=0;i<n;i++)
for(j=0;j<n;j++)
{
if(A[i][j]>A[i][k]+A[k][j])
A[i][j]=A[i][k]+A[k][j];
}
}
开销:
时间复杂度:O(|V|³)
空间复杂度:O(|V|²)
可以用于负权值的图,但是不可以用于带负权值的回路
4 总结
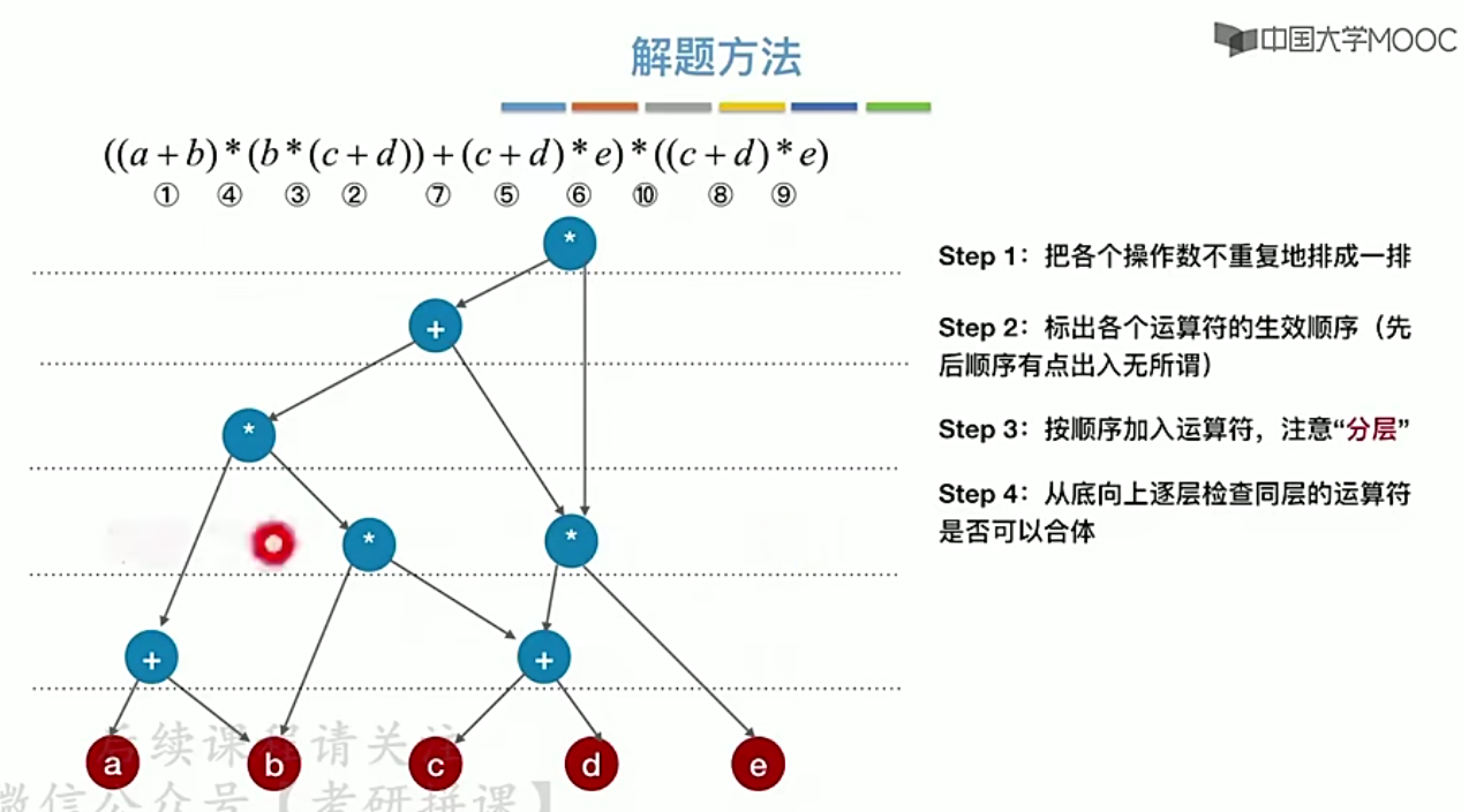
5 有向无环图(DAG:Directed Acyclic Graph)描述表达式
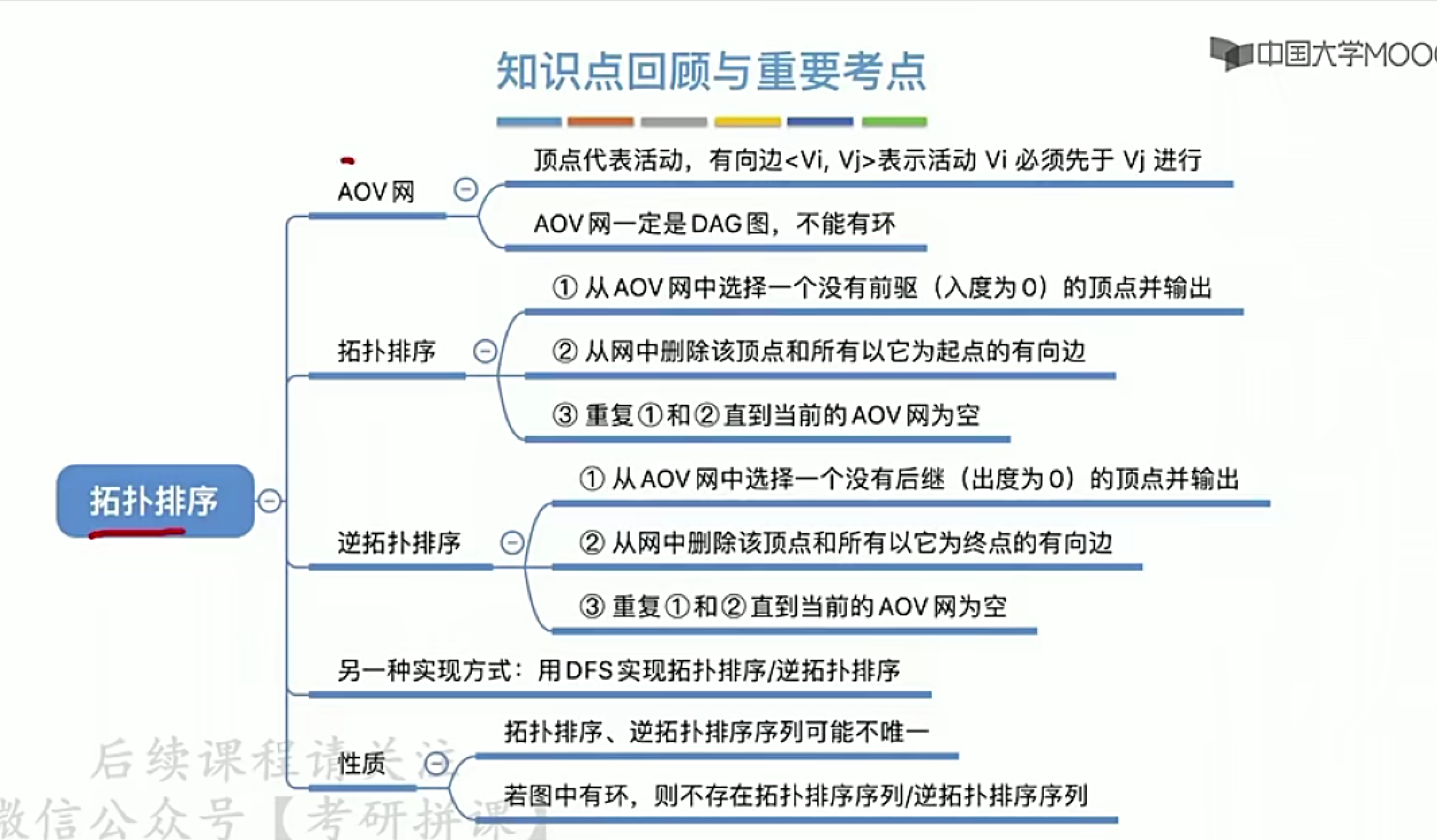
6 拓扑排序
1.AOV网(Activity On Vertex Network):用顶点表示活动的网
2. 拓扑排序代码实现
bool TopoLogicalSort(Graph G)
{
Stack S;
for(int i=0;i<G.vexnum;i++)
{
if(indegree[i]==0)//入度为0的进栈
S.Push(i);
}
int count=0;
while(!S.isEmpty())
{
i=S.Pop();//栈顶元素出栈
print[count++]=i;//记录出栈序列,即为拓扑排序
for(p=G.verticle[i].firstarc;p;p=p->nextarc)//遍历所有与i顶点所连的边
{
v=p->adjvex;//v是顶点i指向的点
if(!(--index[v]))//所有i指向的点的入度都减一
{
S.Push(v);//减完之后入度为0的说明又可以作为下一个入栈的点
}
}//for
}//while
if(count<G.vexnum)//手动画一遍即可知如果有环,会在遍历完所有结点前,栈就空了,因此会提前跳出while循环而导致count值小于G.vexnum
{
return false;//有环
}
else
return true;
}
这是邻接表存储的,时间复杂度为O(|V|+|E|);
如果采用的是邻接矩阵存储则为O(|V|²);
3.逆拓扑排序
-
倒过来,找出度为0的,用临界矩阵或逆邻接表
-
DFS(不咋对,别看了)
- 不带判断环的只要在DFS的最后打印顶点就行
- 带判断的
bool isTree(Graph G) { for(v=0;v<G.vexnum;v++) visited[v]=false; int c=0; int flag=0; for(v=0;v<G.vexnum;v++) { if(!visited[v]) { if(c=1)//说明调用过一次了,再调用就是非连通的,不是一棵树 return false; else { DFS(G,v,&flag); c++; } } } if(flag==1) return false; return true; } void DFS(Graph G,int v,int &flag) { //visit(v); visited[v]=true; for(w=FirstNeighbor(G,v);w>=0;w=NextNeighbor(G,v,w)) { if(visited[w])//访问过,说明有环 { flag=1; } else { DFS(G,w,flag); } } print(v); }
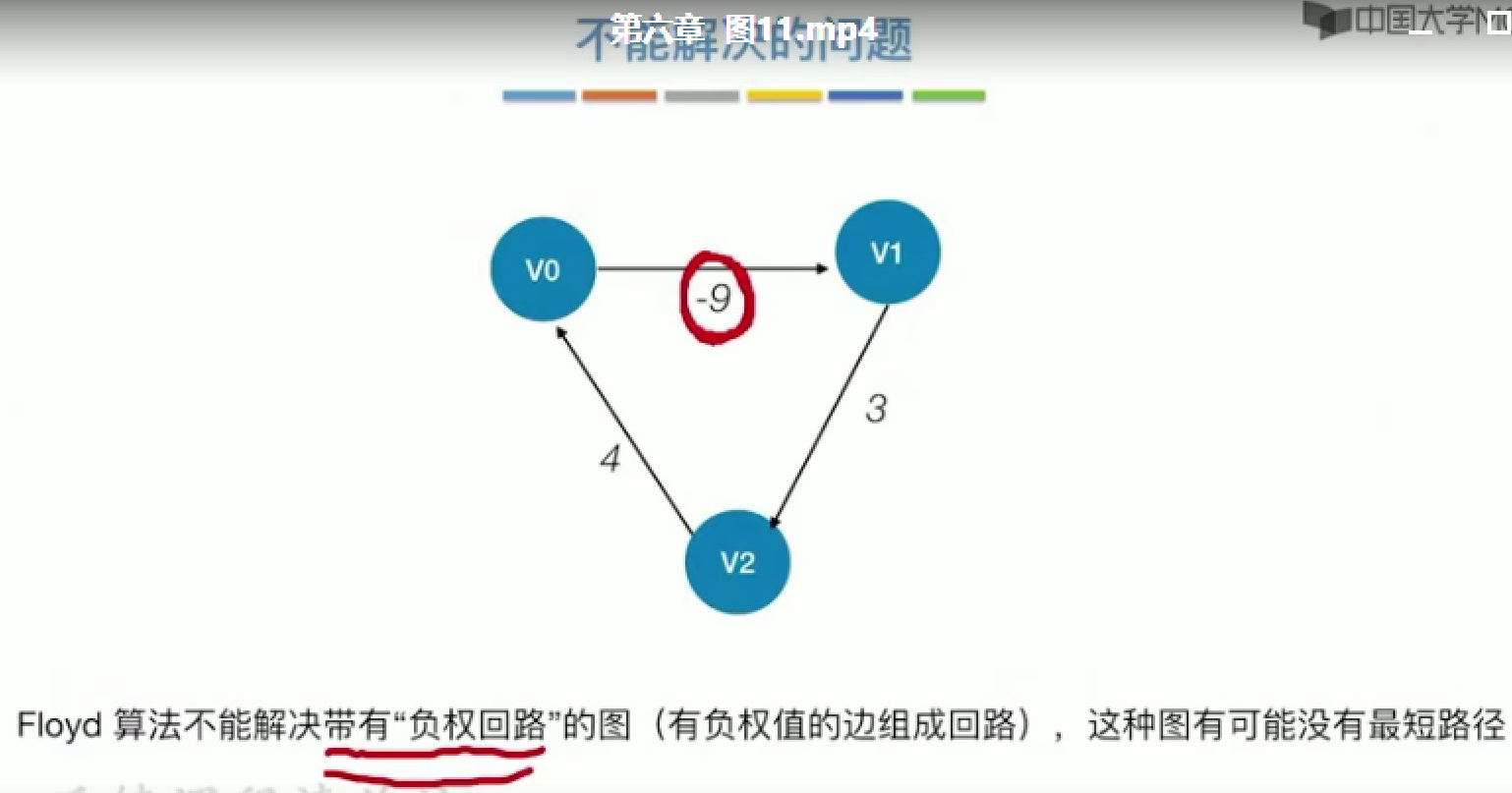
7 关键路径
1 AOE网