第五章 线索二叉树

1.1 线索二叉树

1.1.1 基本概念

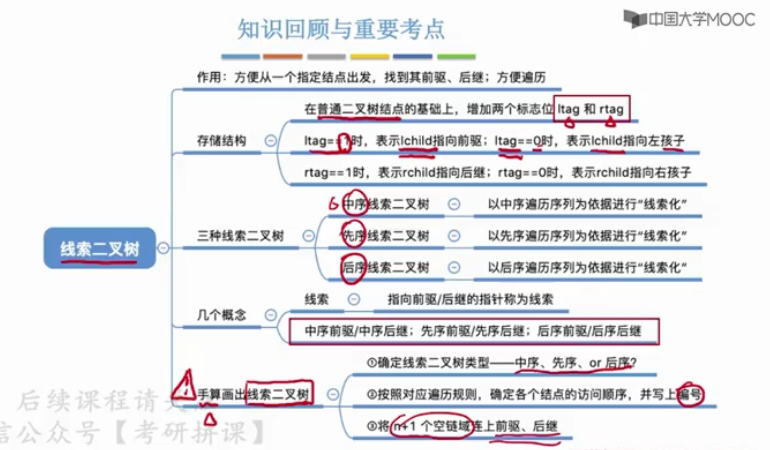
1. 记录前驱和后继是针对某一种遍历来的,不同的遍历方式对某一结点有不同的前驱后继
2. 结点结构
   
3. 标志域含义
   
4. 结点存储结构的代码描述

typedef struct ThreadNode{
    ElemType data;  //数据元素
    struct ThreadNode *lchild,rchild;  //左右孩子指针
    int ltag,rtag;   //左右线索标志
}ThreadNode ,*ThreadTree;

5. 以这种结点构成的二叉链表作为二叉树的存储结构,称为线索链表,指向前驱和后继的指针称为线索,加了线索的二叉树叫做线索二叉树

1.1.2 构造

1.1.2.1 中序线索二叉树的构造

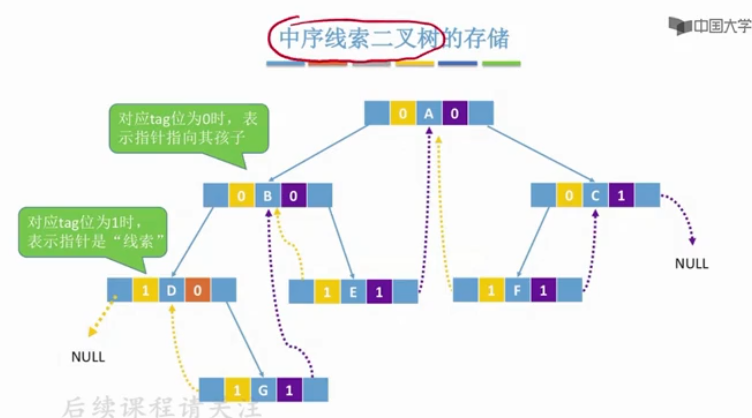
1. 中序遍历找某一结点的前驱

BiNode *pre=NULL;//遍历时的前驱结点
BiNode *final=NULL;//最终的前驱
BiNode * p;//目标结点
void FindPre(BiNode *q)
{
    if(q=p)
        final=pre;找到了
    else
        pre=q;//往下走
}
void InOrder(Bitree T)
{
    InOrder(T->lchild);
    FindPre(T);
    InOrder(T->rchild);
}

2. 中序线索二叉树的构造(实质就是再遍历一遍,然后找符合条件的连一连线)

ThreadNode * pre=NULL;
void visist(ThreadNode *q)//对遍历到的每个结点处理前驱后继
{
    if(q->lchild==NULL)//当前结点的左孩子为空,指向左孩子
    {
        q->child=pre;
        q->ltag=1;
    }
    if(pre!=NULL&&pre->rchild==NULL)//前驱的右孩子为空
    {
        pre->rchild=q;
        pre->rtag=1;
    }
    pre=q;
}
void InThread(ThreadTree T)//中序遍历
{
    InThread(T->lchild);
    visit(T);
    InThread(T->rchild);
}
void CreateThreadTree(Thread T)//中序遍历构造线索二叉树
{
    pre=NULL;
    if(T!=NULL)
    {
        InThread(T);
        pre->rchild=NULL;//处理最后一个结点
        pre->rtag=1;
    }
}

1.1.2.2 先序

和中序的区别不大,但是到最左下角的时候,如果没有左子树了,会指向前驱,但是再到PreThread函数中时,往下执行,会再次返回到他的前驱,然后又到他,死循环

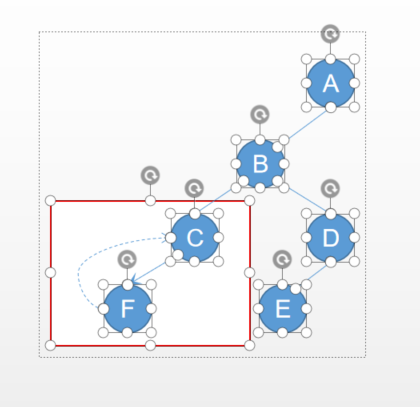
因此需要在其中判断是不是真的指向左子树if(T->ltag==0)

ThreadNode * pre=NULL;
/********visit()函数是一毛一样的****/
void visist(ThreadNode *q)//对遍历到的每个结点处理前驱后继
{
    if(q->lchild==NULL)//当前结点的左孩子为空,指向左孩子
    {
        q->child=pre;
        q->ltag=1;
    }
    if(pre!=NULL&&pre->rchild==NULL)//前驱的右孩子为空
    {
        pre->rchild=q;
        pre->rtag=1;
    }
    pre=q;
}
void PreThread(ThreadTree T)//序遍历
{
    visit(T);
    if(T->ltag==0)//lchild指向的不是线索而是真正的左孩子
        InThread(T->lchild);
    InThread(T->rchild);
}
void CreateThreadTree(Thread T)//先序遍历构造线索二叉树
{
    pre=NULL;
    if(T!=NULL)
    {
        InThread(T);
        pre->rchild=NULL;//处理最后一个结点
        pre->rtag=1;
    }
}

1.1.2.3 后序线索二叉树

visit()一毛一样
PostThread()里顺序改改就行
不同:

void PostThread(ThreadTree T)
{
    PostThread(T->lchild);
    PostThread(T->rchild);
    visit(T);
}

1.1.2.4 小结

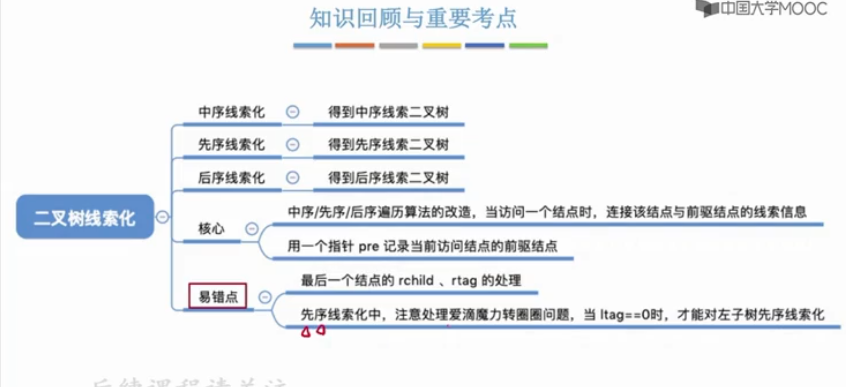
1.1.3 线索二叉树的遍历

1.1.3.1 中序

1. 找某一中序序列下的第一个结点,其实就是给了个子树的根,一直往左下跑

ThreadNode *FirstNode(ThreadNode *p)
{
    while(p->ltag==0)
    {
        p=p->lchild;
    }
    return p;
}