1.1 二叉树的遍历
1.1.1 深度遍历递归算法
- PreOrder
顺序:根->左子树->右子树
void PreOrder(BiTree T)
{
if(T!=NULL)
{
visit(T);
PreOrder(T->lchild);
PreOrder(T->rchild);
}
}
- InOrder
顺序:左子树->根->右子树
void InOrder(BiTree T)
{
if(T!=NULL)
{
InOrder(T->lchild);
visit(T);
InOrder(T->rchild);
}
}
- PostOrder
顺序:左子树->右子树->根
void PostOrder(BiTree T)
{
if(T!=NULL)
{
PostOrder(T->lchild);
PostOrder(T->rchild);
visit(T);
}
}
1.1.2 深度遍历非递归算法
难就难在递归到非递归的转换
- PreOrder
void PreOrder(BiTree T)
{
Stack s;
BiTree p=T;
while(p||!IsEmpty(s))
{
if(p)
{
visit(p);
Push(s,p);
p=p->leftchild;
}
else
{
Pop(s,p);
p=p->rchild;
}
}
}
- InOrder
void InOrder(BiTree T)
{
Stack s;
BiTree p=T;
while(p||!IsEmpty(s))
{
if(p)
{
Push(p);
p=p->lchild;
}
else
{
Pop(p);
visit(p);
p=p->rchild;
}
}
}
- PostOrder
void PostOrder(BiTree T)
{
Stack s;
BiTree p=T;
BiTree r=NULL;
while(p||!sEmpty(s))
{
if(p)
{
Push(s,p);
p=p->lchild;
}
else//没得左子树了
{
Top(s,p);//栈顶元素
if(p->rchild&&p->rchild!=r)//右子树如果存在且没有被访问过
{
p=p->rchild;//把右子树的根结点入栈
Push(s,p);
p=p->lchild;继续转向左子树
}
else//右子树访问过或者不存在右子树,就可以安心地访问这个根结点了
{
Pop(s,p);
visit(p);
r=p;//记录一哈这个访问过了,万一是右子树的根的话,他的老头就会知道自己的右子树访问过了
p=NULL;//p不空的唯一用途就是一直往下寻找左子树,因此置空则是为了表明可以回退去找右子树了
}
}
}
}
1.1.3 一些总结
- 三种遍历算法中,递归遍历左子树,右子树都是固定的,只是访问根结点的顺序不同,不管哪种方式,根结点都访问且仅访问一次,时间复杂度为O(n)
- 空间复杂度和栈的深度有关,最坏是O(n)(一条从上到下)
- 栈的深度是树的深度
- 递归工作栈和非递归用的栈都是
用途(☆):访问p的时候,此时栈内恰好是p结点的所有祖先,从栈底到栈顶再加上p正好构成从根结点到p结点的一条路径.
1.1.4 广度(层次)遍历
自上而下,自左向右的遍历
void LevelOrder(BiTree T)
{
Queue q;
BiTree p=T;
EnQueue(q,p);
while(!IsEmpty(q))//队列非空
{
DeQueue(q,p);
visit(p);
if(p->lchild)
EnQueue(q,p->lchild);
if(p->rchild)
EnQueue(q,p->rchild);
}
}
1.1.5 由遍历序列构造二叉树
- 先序和中序唯一确定一棵二叉树
在先序遍历序列中,第一个结点一定是二叉树的根结点;而在中序遍历中,根结点必然将中序序列分割成两个子序列,前一个子序列是根结点的左子树的中序序列,后一个子序列是根结点的右子树的中序序列。根据这两个子序列,在先序序列中找到对应的左子序列和右子序列。在先序序列中,左子序列的第一个结点是左子树的根结点,右子序列的第一个结点是右子树的根结点。如此递归地进行下去,便能唯一地确定这棵二叉树。
- 先序序列的第一个是根结点(老祖宗),然后在中序序列中从前到后找到老祖宗,根据老祖宗将中序队列划成左子树和右子树的序列
- 左子树再从先序序列找到根(小祖宗了),依次进行,右子树也是......
- 以先序(ABCDEFGHI),中序(BCAEDGHFI)为例
先序中,第一个A,老祖宗,在中序中发现A将BC,EDGHFI隔开,因此左子树是BC,右子树是EDGHFI
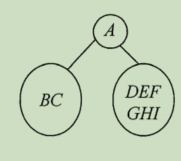
再看BC,先序BC,因此B是根结点,而中序中也是BC,故而C是右子树的
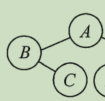
再看右子树EDGHFI,先序是DEFGHI,故而D是根结点,因此在中序中看,D将EDGHFI分成了E和GHFI,E是左子树了
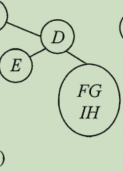
再看GHFI,先序为FGHI,故而F为其根,因此,GH为左子树,I为右子树
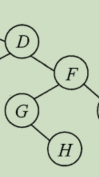
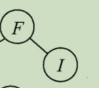
先序后序中GH都是GH的顺序(和刚刚BC的理解一样),因此,G为根,H为右子树
完整是:
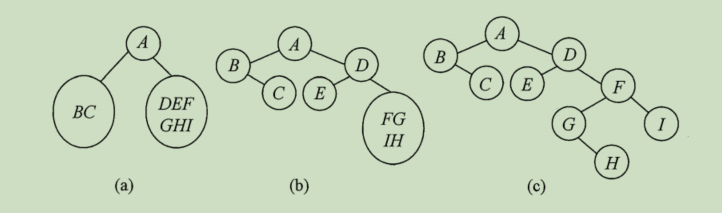
- 后序和中序确定一棵二叉树
和前序中序是差不多的,只是倒过来了,这两种本质都是从先序或后序找到根结点,再到相应的中序中划分成左子树对应的序列,右子树对应的序列,将分好的左右子树序列再带入到先序或后序找到对应的序列,先序就是最左边的是左/右子树的根结点,而后序就是最右边的是左/右子树的根结点 - 层序序列和中序也可以确定
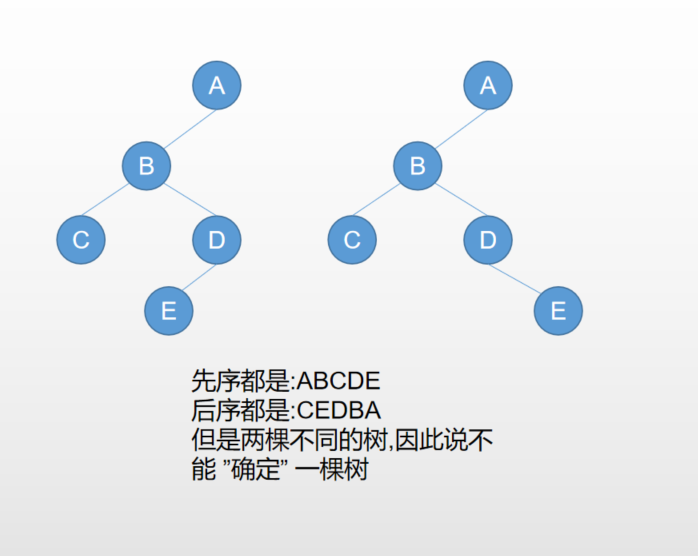
慢慢分析吧,比前面的简单,跟着序列画几个就出来了 - 先序后后序无法确定一棵树